正态分布和标准差的关系原来这么好理解
- 生活
- 2025-09-12
- 104
正态分布和标准差的关系原来这么好理解 大家好呀!今天想和大家聊聊统计学里两个听起来有点吓人但实际上超级有趣的概念——正态分布和标准差。说实话,我刚学的时候也觉得这俩玩意...
正态分布和标准差的关系原来这么好理解
大家好呀!今天想和大家聊聊统计学里两个听起来有点吓人但实际上超级有趣的概念——正态分布和标准差。说实话,我刚学的时候也觉得这俩玩意儿高深莫测,但后来发现它们的关系简直就像咖啡和奶泡一样自然搭配。
先说说正态分布这个"大众脸"
正态分布可以说是统计学界的"大众脸",因为它无处不在。想象一下你们班同学的身高,特别高和特别矮的人总是少数,大多数人都在中间某个范围对吧?这就是正态分布的特点——中间多,两边少,对称得像一个完美的钟形。

我次真正理解正态分布是在大学食堂排队的时候。我发现每天中午12点到12点半是排队高峰期,来得特别早或特别晚的人很少,这不就是一个活生生的正态分布例子吗?从那以后,我开始在生活各处发现正态分布的影子:考试成绩、上班通勤时间、甚至我每天刷手机的时间分布。
标准差就是衡量"胖瘦"的尺子
那么标准差又是什么呢?简单来说,它就是衡量数据分散程度的指标。如果把正态分布比作不同身材的人,标准差就是告诉我们这个人是"苗条"还是"丰满"的尺码。
举个例子,我们班有两个数学考试:
1. A班成绩集中在-分之间,极少数人低于60或高于90
2. B班成绩从50分到100分都有,分布很广
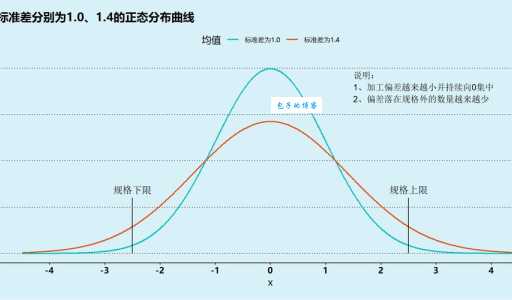
显然,B班成绩的标准差比A班大得多。标准差越大,数据分布就越"胖";标准差越小,数据就越"瘦高"。
两者关系其实很简单
正态分布和标准差的关系可以这样理解:正态分布告诉我们数据大致怎么分布,而标准差则具体量化了这个分布的"胖瘦"程度。
在完美的正态分布中:
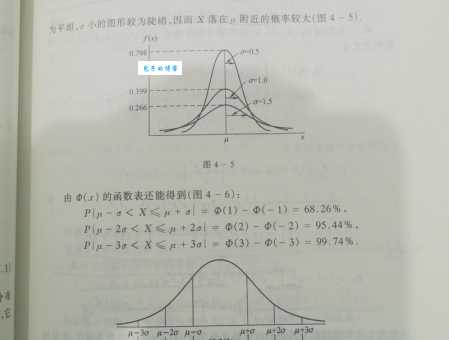
1. 约68%的数据落在均值±1个标准差内
2. 约95%的数据落在均值±2个标准差内
3. 约99.7%的数据落在均值±3个标准差内
这个规律被称为"--99.7法则",我记它的时候就想成是"遛狗-救我-紧急情况"的谐音,虽然有点无厘头,但确实管用。
生活中的实际例子
让我们看一个更具体的例子。假设某城市成年男性平均身高175cm,标准差6cm。那么:
| 范围 | 身高区间 | 占比 |
|---|---|---|
| 均值±1σ | 169cm ~ 181cm | 约68% |
| 均值±2σ | 163cm ~ 187cm | 约95% |
| 均值±3σ | 157cm ~ 193cm | 约99.7% |
从这个表格可以直观看出,标准差越大,这个区间范围就越宽。如果标准差是10cm而不是6cm,那么±1σ的范围就变成了-cm,分布明显更分散了。
为什么这个关系重要?
理解正态分布和标准差的关系在实际生活中特别有用。比如:
1. 质量控制:工厂知道产品尺寸的标准差,就能预测有多少产品可能不符合规格
2. 教育评估:老师可以通过考试成绩的标准差了解试卷区分度
3. 医疗健康:医生用标准差来判断某项指标是否在正常范围内
我记得有一次网购裤子,商家提供了尺码表,包括平均腰围和标准差。通过计算,我准确找到了适合我的尺码,次网购裤子就合身,这是标准差的功劳!
常见误解要避免
刚开始学的时候,我也有过一些错误理解,这里分享给大家避坑:
1. 不是数据都服从正态分布:比如收入分布通常右偏,不是完美的正态
2. 标准差不能单独解释:必须结合均值才有意义,光说"标准差是5"没价值
3. 异常值影响大:极端值会显著增大标准差,分析时要注意
用R语言简单演示
虽然这不是编程教程,但用几行代码可视化这个关系真的很直观:
r
生成两组正态分布数据
set.seed(123)
data1 <- rnorm(1000, mean=50, sd=5)
data2 <- rnorm(1000, mean=50, sd=10)
绘制密度图
plot(density(data1), col="blue", main="不同标准差的比较")
lines(density(data2), col="red")
legend("topright", legend=c("SD=5", "SD=10"), col=c("blue","red"), lty=1)
运行后会看到蓝线(sd=5)比红线(sd=10)更"瘦高",这就是标准差影响的直观体现。
总结一下
正态分布和标准差的关系其实就像剧本和演员的表演范围:正态分布是剧本大纲,规定了故事的基本走向;而标准差则是演员的表演自由度,决定了角色表现的多样性程度。两者配合,才能呈现出一个完整的数据故事。
记住,标准差是描述正态分布"胖瘦"的关键指标,它们共同构成了统计学中强大也实用的工具之一。下次看到新闻报道说"平均工资多少,标准差多少",你就知道怎么解读了!
你们有没有在生活中发现过正态分布和标准差的有趣例子?或者对这两个概念还有什么惑的地方?欢迎在评论区分享你的想法和我们一起讨论!